上篇文章介绍了梯度下降法在线性回归中的相关理论与证明,这里使用程序实例代码方式看梯度下降法是怎样一步一步下降求出最优解的;
X = [1 4;2 5;5 1;4 2];
y = [19;26;19;20];
m = length(y);
alpha = 0.002; %步长
num_iters = 200;
% Init Theta
theta = zeros(2, 1);
% 数据集大小
m = length(y);
% 损失函数记录
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
h= zeros(m,1);
h = X*theta;
J_history(iter) = (1/(2*m))*sum((h-y).^2); %计算每次迭代的损失
tmp1 = zeros(size(X,2),1);
for i=1:m
tmp1= tmp1+(h(i)-y(i)).*X(i,:)'; %等同于公式中累加中的计算结果
end;
theta = theta - (alpha/m)*tmp1; %每次迭代计算theta的值
%disp(J_history(iter));
%disp(theta);
end;
% 绘制图形
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2); %绘制迭代次数于损失值关系图
xlabel('Number of iterations');
ylabel('Cost J');
numel(J_history);
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
expect = 0;
X_p=[4 2]; %预测
expect = theta'*X_p'; %预测结果
Expect
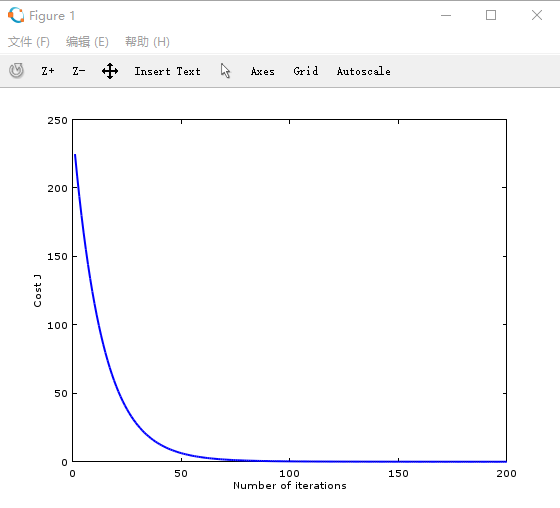
X坐标为迭代次数,Y坐标为损失函数的值,从图中可以看到损失函数下降得很块几乎时线性的,在迭代大约60次的时候损失值已经接近0;这里说的是批量梯度下降法所以数据集有多大也就迭代了多少次;如果数据比较大还是会影响性能,下次有机会再讲讲随机梯度下降法;